5. Оформление графиков функций

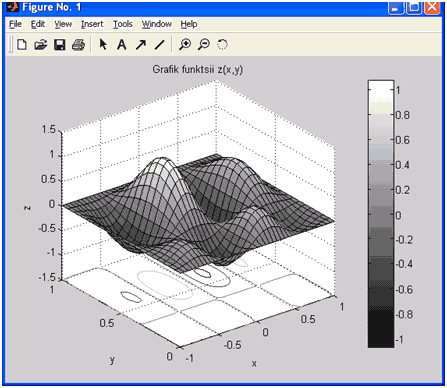
Простым и эффективным способом изменения цветового оформления графика является установка цветовой палитры при помощи функции colormap. Следующий пример демонстрирует подготовку графика функции для печати на монохромном принтере, используя палитру gray.

» surfc(X, Y, Z) 
»colorbar 
» colormap(gray) 
» title('График функции z(x,y)') 
» xlabel('x') 
» ylabel('у') 
» zlabel('z')

Обратите внимание, что команда colormap(gray) изменяет палитру графического окна, т.е. следующие графики будут выводиться в этом окне также в серых тонах. Для восстановления первоначального значения палитры следует применить команду colormap('default'). Цветовые палитры, доступные в MatLab, приведены в табл. 2.

Таблица 2

Палитра	Изменение цвета
autumn	Плавное изменение красный - оранжевый - желтый.
bone	Похожа на палитру gray, но с легким оттенком синего цвета.
colorcube	Каждый цвет изменяется от темного к яркому.
cool	Оттенки голубого и пурпурного цветов.
copper	Оттенки медного цвета.
flag	Циклическое изменение красный - белый - синий - черный.
gray	Оттенки серого.
hot	Плавное изменение черный - красный - оранжевый - желтый - белый.
hsv	Плавное изменение как цветов радуги.
Jet	Плавное изменение синий - голубой - красный - зеленый - желтый - красный.
Pink	Похожа на палитру gray, но с легким оттенком коричневого цвета
Prism	Циклическое изменение красный - оранжевый - желтый - зеленый - синий - фиолетовый.
spring	Оттенки пурпурного и желтого.
summer	Оттенки зеленого и желтого.
Vga	Палитра Windows из шестнадцати цветов.
White	Один белый цвет.
winter	Оттенок синего и зеленого.

6. Вывод нескольких графиков на одни оси

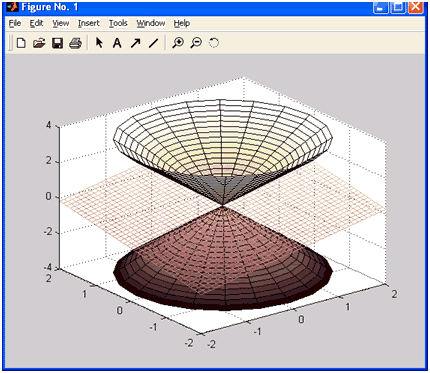
Для отображения нескольких графиков функций одной переменной на одних осях использовались возможности функций plot, plotyy, semilogx, semilogy, loglog. Они позволяют выводить графики нескольких функций, задавая соответствующие векторные аргументы парами, например plot(x,f,x,g). Однако для объединения трехмерных графиков их использовать нельзя. Для объединения таких графиков предназначена команда hold on, которую нужно задать перед построением графика. В следующем примере объединение двух графиков (плоскости и конуса) приводит к их пересечению. Конус задается параметрически следующими зависимостями:

,  ,  ,  .

Для графического отображения конуса сначала необходимо сгенерировать с помощью двоеточия вектор-столбец и вектор-строку, содержащие значения параметров на заданном интервале (важно, что u - вектор-столбец, а v-вектор-строка):

» u = [-2*pi:0.1*pi:2*pi]'; 
» v = [-2*pi:0.1*pi:2*pi];

Далее формируются матрицы  X, Y, содержащие значения функций  и  в точках, соответствующих значениям параметров. Формирование матриц выполняется с помощью внешнего произведения векторов.

Замечание 2

Внешним произведением векторов ,  называется матрица    размера  N x M,  элементы которой вычисляются по формуле  .
Вектор  а  является вектор-столбцом ив MatLab представляется в виде двумерного массива размера N на один. Вектор-столбец bпри транспонировании переходит в вектор-строку размера один на М. Вектор-столбец и вектор-строка есть матрицы, у которых один из размеров равен единице. Фактически, С = abT, где умножение происходит по правилу матричного произведения. Для вычисления матричного произведения в MatLab используется оператор "звездочка". Определим внешнее произведение для двух векторов:

» a = [1;2;3];
» b = [5;6;7];
» C = a*b'
C =
5   6   7
10  12  14
15  18  21

Сформируем матрицы  X,Y, необходимые для графического отображения конуса:

» X = 0.3*u*cos(v); 
» Y = 0.3*u*sin(v);

Матрица Z должна быть того же размера, что и матрицы  X иY. Кроме того, она должна содержать значения, соответствующие значениям параметров. Если бы в функцию  входило произведение и  и  v, то матрицу Z можно было заполнить аналогично матрицам Xи Yпри помощи внешнего произведения. С другой стороны, функцию z(u,v)можно представить в виде , где . Поэтому для вычисления Zможно применить внешнее произведение векторов  и , где вектор-строка  имеет ту же размерность, что v, но состоит из единиц:

» Z = 0.6*u*ones(size(v));

Все требуемые матрицы для отображения конуса созданы. Задание плоскости выполняется следующим образом:

» [X,Y] = meshgrid(-2:0.1:2); 
» Z = 0.5*X+0.4*Y;

Теперь не сложно записать и полную последовательность команд для построения пересекающихся конуса и плоскости:

» u = [-2*pi:0.1*pi:2*pi]'; 
» v = [-2*pi:0.1*pi:2*pi]; 
» X = 0.3*u*cos(v); 
» Y = 0.3*u*sin(v); 
» Z = 0.6*u*ones(size(v));
» surf(X, Y, Z) 
» [X,Y] = meshgrid(-2:0.1:2); 
» Z = 0.5*X+0.4*Y; 
» hold on 
» mesh(X, Y, Z) 
» hidden off

Команда hidden off применена для того, чтобы показать часть конуса, находящуюся под плоскостью. 
Обратите внимание, что команда hold on распространяется на все последующие выводы графиков в текущее окно. Для размещения графиков в новых окнах следует выполнить команду hold off. Команда hold on может применяться и для расположения нескольких графиков функций одной переменной, например,

» plot(x,f,х,g)

эквивалентно последовательности

» plot(х,f) 
» hold on 
» plot(x,g)

Результаты работы, полученные мною: