Операции над нечеткими множествами

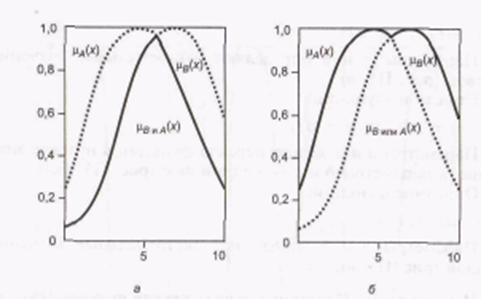
В операции над нечеткими множествами выделяют три основные логические операциинад нечеткими множествами:конъюнкция, дизъюнкция илогическое отрицание. В средеMatlab существует возможность определять конъюнктивные и дизъюнктивные операторы с точки зрения минимаксной и вероятностной интерпретаций.

Рассмотрим минимаксную интерпретацию логических операторов, в которой конъюнктивный оператор представляет нахождение минимума – min (рис. П6, а), а дизъюнктивный – максимум – max (рис. П6, б).

Рис. П6. Пересечение (а) и объединение (б) нечетких множеств 
(минимаксная интерпретация)

Описание конъюнктивной функции: у = min ([у1; у2]).

Описание дизъюнктивной функции: у = тах ([у1; у2]).

Параметры у1 и у2 представляют собой исходные ФП. Функция min работает со списком ФП. В Matlabсписок оформляется квадратными скобками, а элементы списка разделяются точкой с запятой.

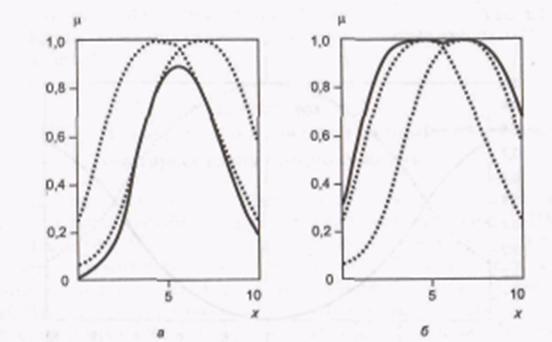
Пример П7. Программа использования операций min и max

x = 0 : 0,1 : 10;
subplot (1, 2, 1); 
y1 = gaussmf (x, [3 5]);
у2 = gaussmf (x, [3 7]);
у3= min ([y1; y2]); 
plot (x, [y1; у2],':');       построение исходных ФП пунктирной линией 
holdon;включение механизма добавления кривой в текущий график
plot (x, у3); 
holdoff;                        выключение механизма добавления кривой в текущий график
subplot (1, 2, 2);
у4 = max([y1; у2]);
plot(x, [y1; у2], ':'); 
hold on;
plot (x, y4);
hold off.

Пунктирной линией на графиках изображены исходные ФП, а сплошной линией – результат действия логических операторов. 
Минимаксная интерпретация является наиболее распространенной при построении нечетких систем. Тем не менее, на практике довольно часто используется альтернативная вероятностная интерпретация конъюнктивных и дизъюнктивных операторов. Matlabсодержит соответствующие функции.

В рамках данной интерпретации конъюнктивный оператор представляет собой оператор вычисления алгебраического произведения – prod(рис. П7, а), а дизъюнктивный оператор – оператор вычисления алгебраической суммы –рrоbоr(рис. П7, б).

Рис. П7. Пересечение (a) и объединение (б) нечетких множеств
(вероятностная интерпретация)

Описание функции:      у = prod ([y1; у2])

Описание функции:      у = probor([y1; у2]).

Параметры y1и у2 представляют собой исходные ФП.

Пример П8. Программа использования вероятностных операторов конъюнкции и дизъюнкции

х = 0 : 0,1 : 10;
subplot (1, 2, 1);
y1 = gaussmf (x, [3 5]); 
y2 = gaussmf (x, [3,7]); 
у3 = prod ([y1; y2]); 
plot(x, [y1; у2],':'); 
hold on; 
plot(x, y3); 
hold off; 
subplot (1, 2, 2); 
y4 = probor ([y1; y2]);
plot (x, [y1; y2], ':');
hold on; 
plot(x, y4);
holdoff.

Рис. П8. Дополнение нечеткого множества.

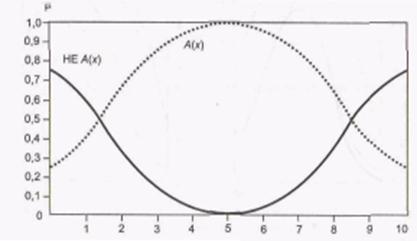
Дополнение нечеткого множества есть не что иное, как математическое представление вербального выражения «НЕ А»(рис. П8), где А – нечеткое множество, описывающее некоторое размытое суждение.

Описание функции дополнения: y = 1 – y*, где у* – исходная ФП.

Пример П9. Программа использования операции дополнения

х = 0 : 0,1 : 10; 
y1 = gaussmf(x, [3 5]); 
у = 1 - y1; 
plot (х, y1, ':'); 
hold on; 
plot(x, y);
hold off.