Урок 5 — Работа с массивами в Матлаб(Matlab)

Все данные MatLab представляет в виде массивов. Очень важно правильно понять, как использовать массивы. Без этого невозможна эффективная работа в MatLab, в частности построение графиков, решение задач линейной алгебры, обработки данных, статистики и многих других. В данном подразделе описаны вычисления с векторами.

Массив - упорядоченная, пронумерованная совокупность однородных данных. У массива должно быть имя. Массивы различаются по числу размерностей или измерений: одномерные, двумерные, многомерные. Доступ к элементам осуществляется при помощи индекса. В MatLab нумерация элементов массивов начинается с единицы. Это значит, что индексы должны быть больше или равны единице.

Важно понять, что вектор, вектор-строка или матрица являются математическими объектами, а одномерные, двумерные или многомерные массивы - способы хранения этих объектов в компьютере. Всюду дальше будут использоваться слова вектор и матрица, если больший интерес представляет сам объект, чем способ его хранения. Вектор может быть записан в столбик (вектор-столбец) и в строку (вектор-строка). Вектор-столбцы и вектор-строки часто будут называться просто векторами, различие будет сделано в тех случаях, если важен способ хранения вектора в MatLab. Векторы и матрицы обозначаются курсивом, а соответствующие им массивы прямым моноширинным шрифтом, например: "вектор а содержится в массиве а", "запишите матрицу R в массив r". 

Ввод сложение и вычитание векторов

Работу с массивами начнем с простого примера - вычисления суммы векторов:
,  .

Для хранения векторов используйте массивы а и b. Введите массив а в командной строке, используя квадратные скобки и разделяя элементы вектора точкой с запятой:

» a = [1.3; 5.4; 6.9] 
a = 
1.3000
5.4000
6.9000

Так как введенное выражение не завершено точкой с запятой, то пакет MatLab автоматически вывел значение переменной а. Введите теперь второй вектор, подавив вывод на экран

» b = [7.1; 3.5; 8.2];

Для нахождения суммы векторов используется знак +. Вычислите сумму, запишите результат в массив  с  и выведите его элементы в командное окно:

» с = а + b 
с =     
8.4000 
8.9000 
15.1000

Узнайте размерность и размер массива а при помощи встроенных функций ndims и size:

» ndims(a) 
ans = 
2 
» size(a)
ans = 
3    1

Итак, вектор а хранится в двумерном массиве а размерностью три на один (вектор-столбец из трех строк и одного столбца). Аналогичные операции можно проделать и для массивов b и c. Поскольку числа в пакете MatLab представляются в виде двумерного массива один на один, то при сложении векторов используется тот же знак плюс, что и для сложения чисел.

Ввод вектор-строки осуществляется в квадратных скобках, однако элементы следует разделять пробелами или запятыми. Операции сложения, вычитания и вычисление элементарных функций от вектор-строк производятся так же, как и с вектор-столбцами, в результате получается вектор-строка того же размера, что и исходные. Например:

» s1 = [3 4 9 2]
s1 = 
3  4  9  2 
» s2 = [5 3 3 2]
s1 = 
5  3  3  2
» s3 = s1 + s2
s3 = 
8  7  12  4

Замечание 1

Если размеры векторов, к которым применяется сложение или вычитание, не совпадают, то выдается сообщение об ошибке.

Естественно, для нахождения разности векторов следует применять знак минус, с умножением дело обстоит несколько сложнее.
Введите две вектор-строки:

» v1 = [2 -3 4 1]; 
» v2 = [7 5 -6 9];

Операция .* (не вставляйте пробел между точкой и звездочкой!) приводит к поэлементному умножению векторов одинаковой длины. В результате получается вектор с элементами, равными произведению соответствующих элементов исходных векторов:

» u = v1.*v2 
u = 
14    -15    -24     9

При помощи .^ осуществляется поэлементное возведение в степень:

» р = v1.^2 
p = 
4   9   16   1

Показателем степени может быть вектор той же длины, что и возводимый в степень. При этом каждый элемент первого вектора возводится в степень, равную соответствующему элементу второго вектора:

» p = vl.^v2 
Р = 
128.0000 -243.0000   0.0002   1.0000

Деление соответствующих элементов векторов одинаковой длины выполняется с использованием операции ./

» d = v1./v2 
d = 
0.2857  -0.6000  -0.6667   0.1111

Обратное поэлементное деление (деление элементов второго вектора на соответствующие элементы первого) осуществляется при помощи операции .\

» dinv = vl.\v2 
dinv = 
3.5000  -1.6667  -1.5000   9.0000

Итак, точка в MatLab используется не только для ввода десятичных дробей, но и для указания того, что деление или умножение массивов одинакового размера должно быть выполнено поэлементно. 
К поэлементным относятся и операции с вектором и числом. Сложение вектора и числа не приводит к сообщению об ошибке. MatLab прибавляет число к каждому элементу вектора. То же самое справедливо и для вычитания:

» v = [4 6 8 10]; 
» s = v + 1.2 
s = 
5.2000  6.2000  9.2000  11.2000
» r = 1.2 - v 
r = 
-2.8000  -4.8000  -6.8000  -8.8000
» r1 = v - 1.2 
r1 = 2.8000 4.8000  6.8000  8.8000

Умножать вектор на число можно как справа, так и слева:

» v = [4 6 8 10]; 
» p = v*2 
р =. 
8   12   16   20 
» pi  = 2*v 
pi = 
8   12   16   20

Делить при помощи знака / можно вектор на число:

» р = v/2 
p = 
2   3   4   5

Попытка деления числа на вектор приводит к сообщению об ошибке:

» р = 2/v 
??? Error using ==> / 
Matrix dimensions must agree.

Если требуется разделить число на каждый элемент вектора и записать результат в новый вектор, то следует использовать операцию ./

» w = [4 2 6]; 
» d = 12./w 
d = 
3  6  2

Все вышеописанные операции применимы как к вектор-строкам, так и к вектор-столбцам. 
Особенность MatLab представлять все данные в виде массивов является очень удобной. Пусть, например, требуется вычислить значение функции sin сразу для всех элементов вектора с (который хранится в массиве с) и записать результат в вектор d. Для получения вектора d достаточно использовать один оператор присваивания:

» d = sin(с) 
d = 
0.8546 
0.5010 
0.5712

Итак, встроенные в MatLab элементарные функции приспосабливаются к виду аргументов; если аргумент является массивом, то результат функции будет массивом того же размера, но с элементами, равными значению функции от соответствующих элементов исходного массива. Убедитесь в этом еще на одном примере. Если необходимо найти квадратный корень из элементов вектора dсо знаком минус, то достаточно записать:

» sqrt(-d) 
ans = 
0 + 0.9244i 
0 + 0.7078i 
0 + 0.7558i

Оператор присваивания не использовался, поэтому пакет MatLab записал ответ в стандартную переменную ans.

Для определения длины вектор-столбцов или вектор-строк служит встроенная функция length:

» length(s1) 
ans = 
4

Из нескольких вектор-столбцов можно составить один, используя квадратные скобки и разделяя исходные вектор-столбцы точкой с запятой:

» v1 = [1; 2];
» v2 = [3; 4; 5]; 
» v = [v1; v2] 
v = 
1
2
3
4
5

Для сцепления вектор-строк также применяются квадратные скобки, но сцепляемые вектор-строки отделяются пробелами или запятыми:

» v1 = [1 2]; 
» v2 = [3 4 5]; 
» v = [v1 v2] 
v = 
1 2 3 4 5

Работа с элементами векторов

Доступ к элементам вектор-столбца или вектор-строки осуществляется при помощи индекса, заключаемого в круглые скобки после имени массива, в котором хранится вектор. Если среди переменных рабочей среды есть массив v, определенный вектор-строкой

» v = [1.3 3.6 7.4  8.2 0.9];

то для вывода, например его четвертого элемента, используется индексация:

» v(4) 
ans = 
8.2000

Появление элемента массива в левой части оператора присваивания приводит к изменению в массиве

» v(2) = 555 
v = 
1.3000 555.0000 7.4000 8.2000 0.9000

Из элементов массива можно формировать новые массивы, например

» u = [v(3); v(2);  v(1)] 
u = 
7.4000
555.0000 
1.3000

Для помещения определенных элементов вектора в другой вектор в заданном порядке служит индексация при помощи вектора. Запись в массив w четвертого, второго и пятого элементов v производится следующим образом:

» ind = [4 2 5];
» w = v(ind) 
w = 
8.2000  555.0000  0.9000

MatLab предоставляет удобный способ обращения к блокам последовательно расположенных элементов вектор-столбца или вектор-строки. Для этого служитиндексация при помощи знака двоеточия. Предположим, что в массиве w, соответствующем вектор-строке из семи элементов, требуется заменить нулями элементы со второго по шестой. Индексация при помощи двоеточия позволяет просто и наглядно решить поставленную задачу:

» w = [0.1 2.9 3.3 5.1 2.6 7.1 9.8]; 
» w(2:6) = 0; 
» w 
w = 
0.1000  0  0  0  0  0  9.8000

Присваивание  w(2:6) = 0  эквивалентно последовательности команд 
w(2) = 0; w(3)=0; w(4)=0; w(5)=0; w(6)=0. 
Индексация при помощи двоеточия оказывается удобной при выделении части из большого объема данных в новый массив:

» w - [0.1 2.9 3.3 5.1 2.6 7.1 9.8]; 
» wl = w(3:5) 
wl = 
3.3000   5.1000   2.6000

Составьте массив w2, содержащий элементы w кроме четвертого. В этом случае удобно использовать  двоеточие и сцепление строк:

» w2 = [w(l:3)  w(5:7)] 
w2 = 
0.1000  2.9000  3.3000  2.6000  7.1000  9.8000

Элементы массива могут входить в выражения. Нахождение, например среднего геометрического из элементов массива u, можно выполнить следующим образом:

» gm = (u(l)*u(2)*u(3))^(l/3) 
gm = 
17.4779

Конечно, этот способ не очень удобен для длинных массивов. Для того чтобы найти среднее геометрическое, необходимо набрать в формуле все элементы массива. В MatLab существует достаточно много специальных функций, облегчающих подобные вычисления.

Применение функций обработки данных к векторам

Перемножение элементов вектора-столбца или вектора-строки осуществляется при помощи функции prod:

» z = [3; 2; 1; 4; 6; 5]; 
» р = prod(z) 
p = 720

Функция sum предназначена для суммирования элементов вектора. С ее помощью нетрудно вычислить среднее арифметическое элементов вектора z:

» sum(z)/length(z) 
ans = 
3.5000

В MatLab имеется и специальная функция mean для вычисления среднего арифметического:

» mean(z) 
ans = 
3.5000

Для определения минимального и максимального из элементов вектора служат встроенные функции min и max:

» m1 = max(z) 
m1 = 
6 
» m2 = min(z) 
m2 = 
1

Часто необходимо знать не только значение минимального или максимального элемента в массиве, но и его индекс (порядковый номер). В этом случае встроенные функции min и max необходимо использовать с двумя выходными аргументами, например

» [m, k] = min(z) 
m = 
1 
k = 
3

В результате переменной m будет присвоено значение минимального элемента массива z, а номер минимального элемента занесен в переменную k.
Для получения информации о различных способах использования функций следует набрать в командной строке help и имя функции. MatLab выведет в командное окно всевозможные способы обращения к функции с дополнительными пояснениями. 
В число основных функций для работы с векторами входит функция упорядочения вектора по возрастанию его элементов sort.

» r = [9.4 -2.3 -5.2 7.1 0.8 1.3]; 
» R = sort(r) 
R =  
-5.2000  -2.3000  0.8000  1.3000  7.1000  9.4000

Можно упорядочить вектор по убыванию, используя эту же функцию sort:

» R1 = -sort(-r) 
R1 = 
9.4000  7.1000  1.3000  0.8000  -2.3000  -5.2000

Упорядочение элементов в порядке возрастания их модулей производится с привлечением функции abs:

» R2 = sort(abs(r)) 
R2 = 
0.8000  1.3000  2.3000  5.2000  7.1000  9.4000

Вызов sort с двумя выходными аргументами приводит к образованию массива индексов соответствия элементов упорядоченного и исходного массивов:

» [rs, ind] = sort(r) 
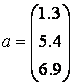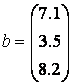rs =   
-5.2000  -2.3000  0.8000  1.3000  7.1000  9.4000 
ind = 
3    2    5    6    4    1