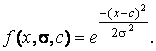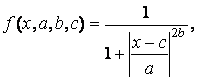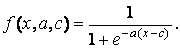Способы формирования нечетких множеств

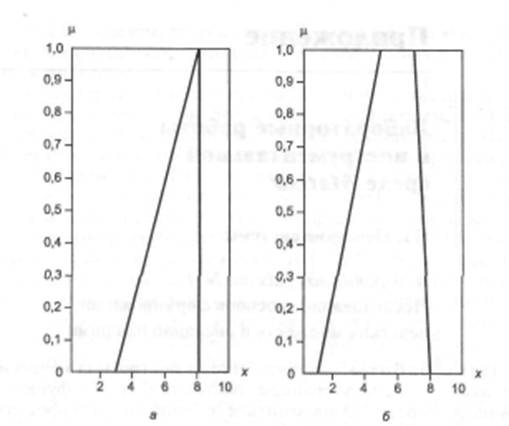
Функции принадлежности

Инструментарий нечеткой логики (ИНЛ) в составе пакета Matlabсодержит 11 встроенных типов функций принадлежности (ФП), формируемых на основе кусочно-линейных функций, распределения Гаусса, сигмоидной кривой, квадратических и кубических полиномиальных кривых. К наиболее простым ФП можно отнести треугольную и трапециевидную. Наименование треугольной ФП – trimf (trianglemembership function). В параметрическом виде она представляет собой не что иное, как набор трех точек, образующих треугольник.

Описание функции:у = trimf(x,[abс]),

где вектор х – базовое множество, на котором определяется ФП. Величины а и с задают основание треугольника, b– его вершину.
В аналитическом виде треугольная ФП может быть задана следующим образом (рис. П1, а):

Рис. П1. Треугольная (а) и трапециевидная (б) функции принадлежности

Далее рассмотрим примеры использования различных ФП в системе.

Примеры представляют собой фрагменты программ и комментариев на языке пакетаMatlab.

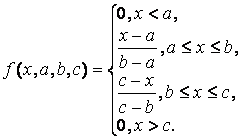
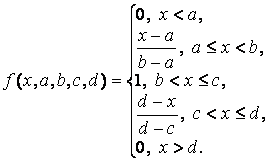
Пример П1. Программа использования ФП trimf

х = 0 : 0,1 : 10;                               Задается базовое множество 
у = trimf(x, [3 6 8]);                         Определяется треугольная ФП 
plot (х, у) ;                                                   Выводится график функции
xlabel('trimf(x, P), P = [3 6 8]');     Подписывается график под осью абсцисс 

Трапециевидная ФП - trapmf (trapezoid membership function) – отличается от предыдущей функции лишь тем, что имеет верхнее основание.

Описание функции: у = trapmf(х, [abс d]),
где параметры    а и d – нижнее основание трапеции; 
b и с –верхнее основание трапеции (рис. П1, б). 

Аналитическая запись трапециевидной функции имеет вид: 
 

Одно из основных достоинств треугольных и трапециевидных ФП – их простота. На основе функции распределения Гаусса можно построить ФП двух видов: простую функцию принадлежности Гаусса и двухстороннюю, образованную с помощью различных функций распределения Гаусса. Первая из них обозначается gaussmf, а вторая – gauss2mf.

Описание функции: 
у = gaussmf(x, [, с]). 

Симметричная функция Гаусса зависит от двух параметров и с (рис. П.2, а): 

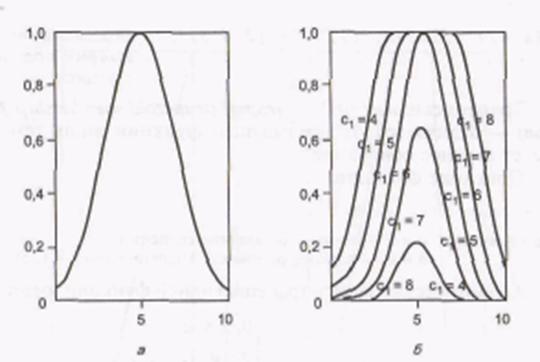
Пример П2. Программа использования ФП gaussmf

X= 0 : 0,1 : 10; 
Y= gaussmf(х, [2 5]); 
plot (х, у);

Рис. П2. Простая (а) и двухсторонняя (б) функции принадлежности Гаусса.

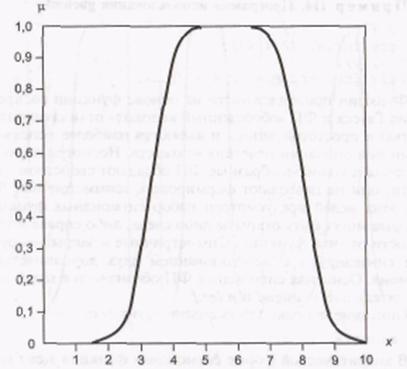
Описание функции: у = gauss2mf (x, [1, с1, 2, c2]). 
Последнее выражение является комбинацией двух различных функций распределения Гаусса. Первая определяется параметрами 1 и с1 и задает форму левой стороны, а вторая (параметры 2, c2) – правой стороны ФП.

Если с1 < c2, то в этом случае функция gauss2mf достигает своего максимального значения на уровне 1. Иначе – максимальное значение функции меньше 1 (рис. П2,б).

Пример ПЗ. Программа использования ФП gauss2mf

х = (0 : 0,1 : 10)'; 
y1 = gauss2mf(x, [2 4 1 8]);
у2 = gauss2mf(x, [2 5 1 7]);
уЗ = gauss2mf(x, [2 6 1 6]);
у4 = gauss2mf(x, [2 7 1 5]); 
У5 = gauss2mf(x, [2 8 1 4]); 
Plot (x, [y1 у2 уЗ у4 у5]);

Символ «'» в строке определения базового множества х показывает транспонированность базового множества. 
Следующей функцией, которая позволяет представлять нечеткие субъективные предпочтения, является ФП «обобщенный колокол» и обозначаетсяgbellmf(generalized bell shape membership function).

 
gbellmf, P = [2 4 6]
Рис. П3. Функция принадлежности «обобщенный колокол»

Ее отличие от рассмотренных ранее ФП заключается в добавлении третьего параметра, что позволяет осуществлять плавный переход между нечеткими множествами.

Описание функции: у = gbellmf (x, [а b с]) . 
Функция «обобщенный колокол» зависит от трех параметров и имеет следующую аналитическую запись:

где с – определяет расположение центра ФП; а и b – оказывают влияние на форму кривой (рис. ПЗ).

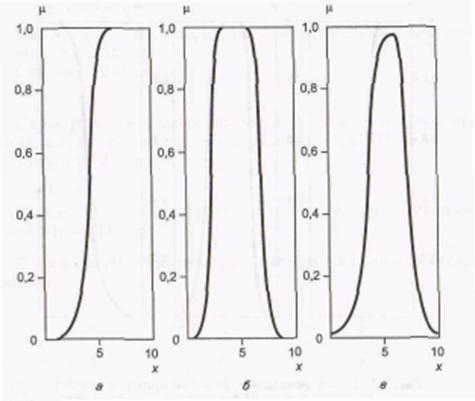
Пример П4. Программа использования gbellmf

х = 0 : 0,1 : 10; 
у = gbellmf (х, [2 4 6]);
plot(x, у); 
xlabel('gbellmf, р = [2 4 61]').

Функции принадлежности на основе функции распределения Гаусса и ФП “обобщенный колокол” отличаются гладкостью и простотой записи и являются наиболее используемыми при описании нечетких множеств. Несмотря на то, что гауссовы и колоколообразные ФП обладают свойством гладкости, они не позволяют формировать асимметричные ФП. Для этих целей предусмотрен набор сигмоидных функций, которые могут быть открыты либо слева, либо справа в зависимости от типа функции. Симметричные и закрытые функции синтезируют с использованием двух дополнительных сигмоид. Основная сигмоидная ФП обозначается sigmf, а дополнительные – dsigmf и psigmf.

Описание основной сигмоидной функции: у = sigmf (х, [a с]). 
В аналитической форме сигмоидная функция sigmf записывается следующим образом: 

В зависимости от знака параметра a рассматриваемая ФП будет открыта или справа или слева (рис. П4, а), что позволит применять ее при описании таких нечетких понятий, как «очень большой», «крайне отрицательно» и др.

Описание дополнительной сигмоидной функции: у = dsigmf(x, (a1, c1, а2, с2)) .
ФП dsigmf зависит от четырех параметров a1, c1, а2 и с2 и определяется как разность двух сигмоидных функций: f(х, a1, c1) - f(x, а2, с2) (рис. П4, б).

Описание дополнительной сигмоидной функции: у = psigmf (x, [a1, c1, а2, с2]) .

ФП psigmf, так же как и предыдущая функция, зависит от четырех параметров a1, c1, а2, с2 и определяется как произведение двух сигмоидных функцийf(х, a1, c1)*f(x, а2, с2) (рис. П4, в).

Рис. П4. Сигмоилные функции принадлежности: 
а – основная односторонняя; б – дополнительная двухсторонняя; 
в — дополнительная несимметричная

Пример П5. Программа  использования сигмоидных функций

х = 0 : 0,1 : 10;                      определяется базовое множество 
subplot (1, 3, 1);                     формируется матрица графиков (3x1)
                                               первый элемент – текущий 
y=sigmf(x,[2 4]);
plot (х, у);                               выводится график в первый элемент матрицы 
xlabel ('sigmf, P = [2 4]') 
subplot (1, 3, 2);                     выбирается второй текущий элемент
у = dsigmf (x, [5 2 5 7]);
plot (х, у);                               выводится график во второй элемент матрицы
xlabel ('dsigmf, Р = [5 2 5 7]') 
subplot (1, 3, 3);                     выбирается третий текущий элемент
у = psigmf (x, [2 3 -5 8]); 
plot (х, у);                               выводится график в третий элемент матрицы
xlabel ('psigmf, P= [2 3 -5 8]');

Рис. П5. Полиномиальные функции принадлежности:
а – Z-функция; б – PI-функикя; в – S-функиия 

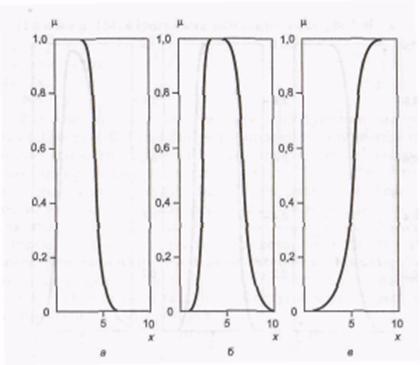
Инструментарий нечеткой логики (fuzzy logic toolbox) в составеMatlabпредоставляет возможность формирования ФП на основе полиномиальных кривых. Соответствующие функции называются Z-функции (zmf), РI-функции (pimf)и S-функции (smf). Функция zmfпредставляет собой асимметричную полиномиальную кривую, открытую слева (рис. П5, а), функция smf – зеркальное отображение функции zmf (рис. П5, в). Соответственно функция pimf равна нулю в правом и левом пределах и принимает значение, равное единице, в середине некоторого отрезка (рис. П5, б).

Описание функции: у = zmf(x, [ab]). 
Параметры а и b определяют экстремальные значения кривой (рис. П5, а).

Описание функции: у = pimf (x, [ab с d]). 
Параметры а и dзадают переход функции в нулевое значение, а параметры bи с – в единичное (рис. П5, б).

Описание функции: у = smf (х, [а b]) . 
Параметры а и bопределяют экстремальные значения кривой (рис. П5, в).

Пример П6. Программа использования полиномиальных кривых

х = 0 : 0,1 : 10;
subplot(1, 3, 1);
у = zmf(x, (3 7]);
plot (х, у);
xlabel (' zmf, P = [3 7]');
subplot (1, 3, 2);
у = pimf(x, [1 4 5 10]);
plot (x, у);
xlabel ('pimf, P = [1 4 5 10]');
subplot (1, 3, 3);
у = smf (x, [1 8]);
plot(x, y);
xlabel ('smf, P=[1 8]').

Помимо рассмотренных выше функций, позволяющих представлять нечеткие множества, в Mattabимеется возможность формировать собственные ФП или модифицировать встроенные.