Урок 6 — Матрицы. Работа с матрицами в MatLab. Примеры
|
1. Различные способы ввода матриц в пакете MatLabВводить небольшие по размеру матрицы удобно прямо из командной строки. Введите матрицу размерностью два на три
Для хранения матрицы используйте двумерный массив с именем A. При вводе учтите, что матрицу А можно рассматривать как вектор-столбец из двух элементов, каждый из которых является вектор-строкой длиной три, следовательно, строки при наборе отделяются точкой с запятой: » А = [3 1 -1; 2 4 3] Для изучения простейших операций над матрицами приведем еще несколько примеров. Рассмотрим другие способы ввода. Введите квадратную матрицу размера три так, как описано ниже:
Начните набирать в командной строке » В = [4 3 -1 Нажмите клавишу <Enter>. Обратите внимание, что пакет ничего не вычислил. Курсор мигает на следующей строке без символа ». Продолжите ввод матрицы построчно, нажимая в конце каждой строки <Enter>. Последнюю строку завершите закрывающей квадратной скобкой, получается: 2 7 0 Еще один способ ввода матриц состоит в том, что матрицу можно трактовать как вектор-строку, каждый элемент которой является вектор-столбцом. Например, матрицу два на три
можно ввести при помощи команды: » С = [[3; 4] [-1; 2] [7; 0]] Посмотрите переменные рабочей среды, набрав в командной строке whos: А 2x3 48 double array Итак, в рабочей среде содержится три матрицы, две прямоугольные и одна квадратная. 2. Обращение к элементам матриц в пакете MatLabДоступ к элементам матриц осуществляется при помощи двух индексов - номеров строки и столбца, заключенных в круглые скобки, например » С(2, 3) Элементы матриц могут входить в состав выражений: » С(1, 1) + С(2, 2) + С(2, 3) Расположение элементов матрицы в памяти компьютера определяет еще один способ обращения к ним. Матрица А размера m на n хранится в виде вектора длиныmn, в котором элементы матрицы расположены один за другим по столбцам [А(1,1) А(2,1) ... А(m,1) ... А(1,n) А(2,n) ... А(m,n)]. Для доступа к элементам матрицы можно использовать один индекс, задающий порядковый номер элемента матрицы в векторе. [C(1,1) C(2,1) C(1,2) С(2,2) С(1,3) С(2,3)], который имеет шесть компонент. Доступ к элементам матрицы осуществляется следующим образом: » С(1) 3. Операции над матрицами в пакете MatLab: сложение, вычитание, умножение, транспонирование и возведение в степеньПри использовании матричных операций следует помнить, что для сложения или вычитания матрицы должны быть одного размера, а при перемножении число столбцов первой матрицы обязано равняться числу строк второй матрицы. Сложение и вычитание матриц, так же как чисел и векторов, осуществляется при помощи знаков плюс и минус. Найдите сумму и разность матриц С и А,определенных выше: » S = А+С Следите за совпадением размерности, иначе получите сообщение об ошибке: » S = А+В Для умножения матриц предназначена звездочка: » Р = С*В Умножение матрицы на число тоже осуществляется при помощи звездочки, причем умножать на число можно как справа, так и слева: » Р = А*3 Транспонирование матрицы, так же как и вектора, производится при помощи .', а символ ' означает комплексное сопряжение. Для вещественных матриц эти операции приводят к одинаковым результатам: » В' » В.' Замечание 1 Если матрица Сопряжение и транспонирование матриц, содержащих комплексные числа, приведут к созданию разных матриц: »K= [l-i, 2+3i; 3-5i, l-9i] » K.' Замечание 2 При вводе вектор-строк их элементы можно разделять или пробелами, или запятыми. При вводе матрицы К применены запятые для более наглядного разделения комплексных чисел в строке. Возведение квадратной матрицы в целую степень производится с использованием оператора ^: » В2 = В^2 Проверьте полученный результат, умножив матрицу саму на себя. (A + С) В3 (A-С)Т. Учтите приоритет операций, сначала выполняется транспонирование, потом возведение в степень, затем умножение, а сложение и вычитание производятся в последнюю очередь. »(А+С)*В^3*(А-С)' 4. Умножение матриц и векторовВектор-столбец или вектор-строка в MatLab являются матрицами, у которых один из размеров равен единице, поэтому все вышеописанные операции применимы и для умножения матрицы на вектор-столбец или вектор-строки на матрицу. Например, вычисление выражения можно осуществить следующим образом: » a = [1 3 -2]; 5. Блочные матрицыОчень часто в приложениях возникают так называемые блочные матрицы, т.е. матрицы, составленные из непересекающихся подматриц (блоков). Рассмотрим вначале конструирование блочных матриц. Введите матрицы: » К = [А В; С D] Блочную матрицу можно получить и другим способом, если считать, что матрица Ксостоит из двух столбцов, в первом - матрицы А и С, а во втором - В и D: » К = [[А; С] [В; D]] Обратной задачей к конструированию блочных матриц является задача выделения блоков. Выделение блоков матриц осуществляется индексацией при помощи двоеточия. Введите матрицу
и затем выделите подматрицу с элементами »Р1 = Р(2:3,2:3) Для выделения из матрицы столбца или строки (то есть массива, у которого один из размеров равен единице) следует в качестве одного из индексов использовать номер столбца или строки матрицы, а другой индекс заменить двоеточием без указания пределов. Например, запишите вторую строку матрицы Р в вектор р »p = P(2, :) При выделении блока до конца матрицы можно не указывать ее размеры, а использовать элемент end: »p = Р(2, 2:end) 6. Удаление строк и столбцовВ MatLab парные квадратные скобки [ ] обозначают пустой массив, который, в частности, позволяет удалять строки и столбцы матрицы. Для удаления строки следует присвоить ей пустой массив. Удалите, например, первую строку квадратной матрицы: » М = [2 0 3 Обратите внимание на соответствующее изменение размеров массива, которое можно проверить при помощи size: » size(M) Аналогичным образом удаляются и столбцы. Для удаления нескольких идущих подряд столбцов (или строк) им нужно присвоить пустой массив. Удалите второй и третий столбец в массиве M » М(:, 2:3) = [] Индексация существенно экономит время при вводе матриц, имеющих определенную структуру. 7. Заполнение матриц при помощи индексацииВыше было описано несколько способов ввода матриц в MatLab. Однако часто бывает проще сгенерировать матрицу, чем вводить ее, особенно если она обладает простой структурой. Рассмотрим пример такой матрицы:
Генерация матрицы Т осуществляется в три этапа: » A(1:5, 1:5) = 0 Создание некоторых специальных матриц в MatLab осуществляется при помощи встроенных функций. 8. Создание матриц специального видаЗаполнение прямоугольной матрицы нулями производится встроенной функцией zeros, аргументами которой являются число строк и столбцов матрицы: » A = zeros(3, 6) Один аргумент функции zeros приводит к образованию квадратной матрицы заданного размера: » A = zeros(3) Единичная матрица инициализируется при помощи функции eye: » I = eye(4) Функция eye с двумя аргументами создает прямоугольную матрицу, у которой на главной диагонали стоят единицы, а остальные элементы равны нулю: » I = eye(4, 8) Матрица, состоящая из единиц, образуется в результате вызова функции » E = ones(3, 7) Использование одного аргумента в ones приводит к созданию квадратной матрицы, состоящей из единиц. MatLab предоставляет возможность заполнения матриц случайными элементами. Результатом функции rand является матрица чисел, распределенных случайным образом между нулем и единицей, а функции randn — матрица чисел, распределенных по нормальному закону: » R = rand(3, 5) Один аргумент функций rand и randn приводит к формированию квадратных матриц: » d = [1; 2; 3; 4]; Функция diag служит и для выделения диагонали матрицы в вектор, например » A = [10 1 2; 1 20 3; 2 3 30]; 9. Поэлементные операции с матрицамиПоскольку векторы и матрицы хранятся в двумерных массивах, то применение математических функций к матрицам и поэлементные операции производятся так же, как для векторов.
Умножение каждого элемента одной матрицы на соответствующий элемент другой производится при помощи оператора .*: » С = А.*В Для деления элементов первой матрицы на соответствующие элементы второй используется оператор ./, а для деления элементов второй матрицы на соответствующие элементы первой служит .\: » R1 = А./В1 Поэлементное возведение в степень осуществляется при помощи оператора .^. Показатель степени может быть числом или матрицей того же размера, что и матрица, возводимая в степень. Во втором случае элементы первой матрицы возводятся в степени, равные элементам второй матрицы. 10. Визуализация матрицМатрицы с достаточно большим количеством нулей называются разреженными.Часто необходимо знать, где расположены ненулевые элементы, т.е. получить так называемый шаблон матрицы. Для этого в MatLab служит функция spy. Посмотрим шаблон матрицы G » spy(G) После выполнения команды spy на экране появляется графическое окно Figure No. 1. На вертикальной и горизонтальной осях отложены номера строк и столбцов. Ненулевые элементы обозначены маркерами, внизу графического окна указано число ненулевых элементов (nz = 19). » imagesc(G) В результате получается наглядное представление матрицы. |

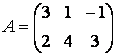 .
.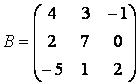 .
.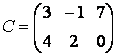

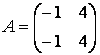 ,
, 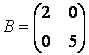 ,
, 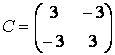 ,
, 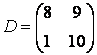 и создайте из них блочную матрицу
и создайте из них блочную матрицу 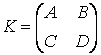 .
. 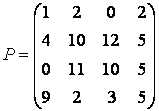
 .
.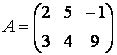 ,
, 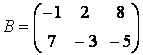 .
. .
.